About Me

Yiming Shen is a Ph.D. Candidate in Applied & Computational Mathematics at the University of Massachusetts Boston, conducting research under Prof. David Degras-Valabregue.

Specializing in Statistical Modeling and Healthcare Data Science, my work bridges the gap between rigorous mathematical derivation and actionable clinical insights. I focus on developing high-dimensional data analysis methods for Brain-Computer Interfaces (BCI) and Medical Imaging.

I am actively seeking Data Scientist roles in the Pharmaceutical and Biotechnology industries.

Technical Expertise

Statistical Learning & Modeling

High-dimensional Tensor Analysis, Bayesian Inference, Mixed-Effects Models, Survival Analysis.

Machine Learning & BCI

Deep Learning for EEG/MRI, Domain Adaptation, Riemannian Geometry, Feature Engineering (CSP, Log-variance).

Computational Tools

R (Expert, Package Development), Python (scikit-learn, PyTorch), SQL, LaTeX, Git.

Selected Achievements

Kaggle Silver Medal (2024) | HMS - Harmful Brain Activity Classification

• Developed a robust pipeline to detect seizures in complex EEG data, achieving a Top 5% ranking globally.
• View Project Detail

R Package Developer | DA4BCI

• Authored Data Augmentation for BCI, an R package optimizing classification accuracy for motor imagery tasks using geometric data generation.
• View Repository

Research Framework

My research integrates High-Dimensional Tensor Analysis with Riemannian Manifold Geometry to solve the fundamental challenge of neurophysiological non-stationarity in Brain-Computer Interfaces (BCI). This framework is structured around three theoretical pillars:

High-Dimensional Tensor MCCA

Developed computational methods for Tensor Multiple Canonical Correlation Analysis (TMCCA) capable of handling datasets of arbitrary and mixed orders. This work establishes a statistical framework for integrating multi-view neuroimaging data.

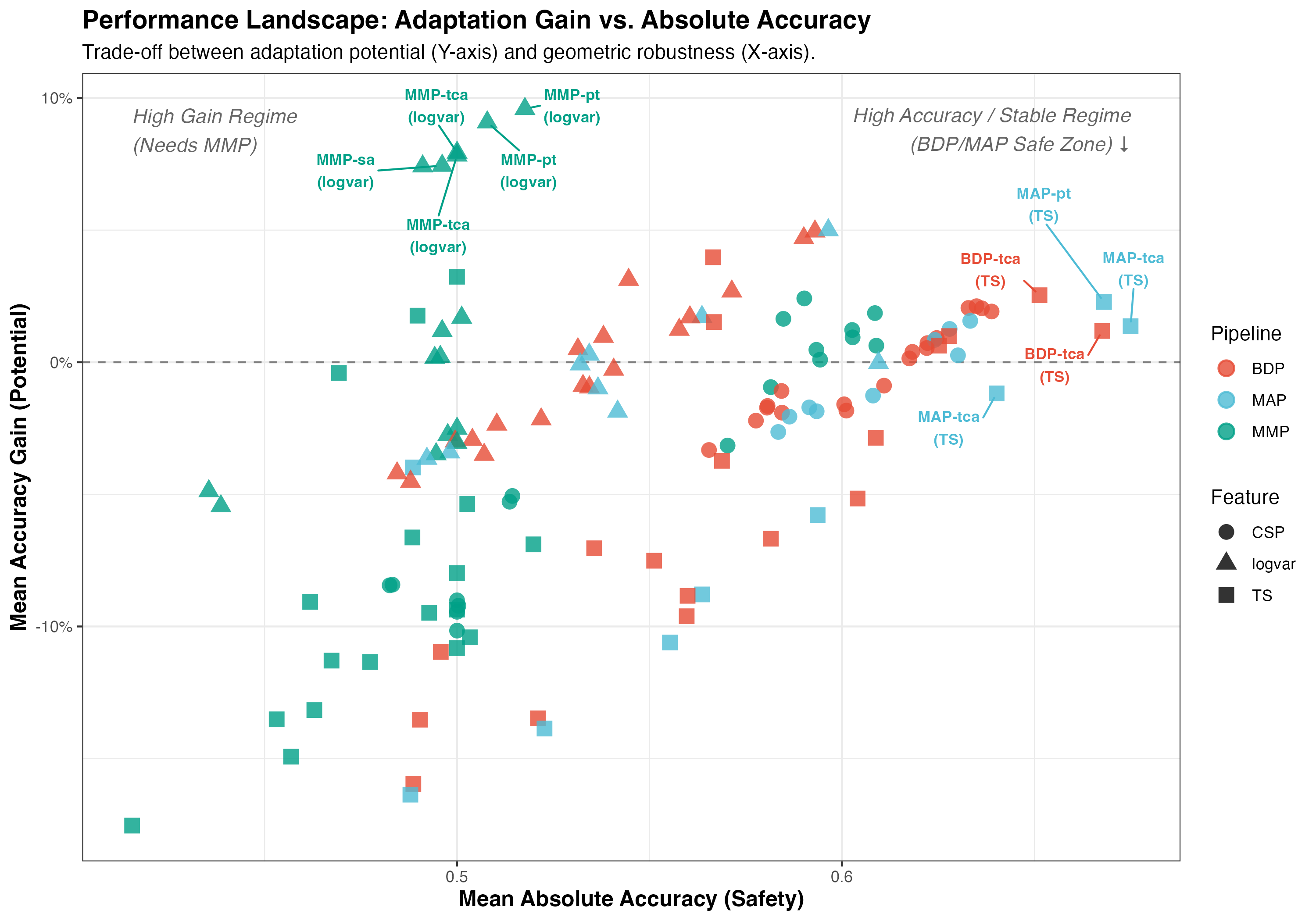
Geometric Decomposition of Neural Drift

Analyzed EEG covariance evolution on the Riemannian manifold of Symmetric Positive Definite (SPD) matrices. By projecting representations onto a common unit-trace SPD manifold, I isolate geometric structural distortions from signal magnitude changes to diagnose performance decay.

Confidence-Gated Adaptive Decoding

Reframed BCI adaptation as a statistically grounded decision problem. Using Confidence-Interval (CI) Gating and Non-Inferiority Testing, this framework selects optimal adaptation pipelines (e.g., Bridge-Domain vs. Minimum-Distance) based on measured neurophysiological divergence.